빠르게 소수 판별하기 2

1. main.zip(전체 소스코드)

안녕하세요? noname01입니다. 지난 번에 캐시를 활용해서 소수를 빠르게 판별하는 방법에 대한 글을 썼었죠. 바로 다음 글입니다.

캐시를 이용해 빠르게 소수 판별하기

이 글을 보신 열심히해보자님께서 새로운 두 편의 글을 써 주셨습니다. 바로 다음 글입니다(다음 글들을 이해하지 못하면 이 글도 이해할 수 없으므로, 이 글을 읽기 전에 다음 글들을 먼저 이해한 후 이 글을 읽어주시기 바랍니다).

소수 빠르게 구하기 (소프트웨어 놀이터 네이버 카페의 열심히해보자 님의 글입니다)

아주 큰 수(UINT64_MAX 범위 안의)까지 특정 구간에서 소수를 빠르게 찾아주는 프로그램소스입니다. (마찬가지로, 열심히해보자 님의 글입니다)

열심히해보자 님이 쓰신 글의 핵심 내용은 에라토스테네스의 체를 비트 단위로 쪼개서 구현하여 최적화를 하는 것입니다. 개인적으로 정말 멋진 아이디어라고 생각합니다. 이 방법을 통해서 비트 배열을 만들어 놓고, 어떤 정수 n이 소수인지 판별하려면 다음과 같이 하면 끝입니다(실제로는 비트 연산을 통해 인덱스 계산을 해야 하므로 아래와 다릅니다. 아래 문장은 그냥 개념적으로 그렇단 말입니다).

bit_ary[n] == true;(실제로 구현 방법에 따라서는 false이어야 소수가 될 수도 있습니다. 열심히해보자님의 코드와 제가 작성한 코드에서는 true대신 false로 소수를 표시합니다)

물론 메모리 사용량도 크게 아낄 수 있습니다. 그런데, 이 방법에도 단점이 없는 것은 아닙니다. 비트 단위로 쪼개서 구현을 하게 되면, 특정 정수가 소수인지를 판별하는 방법은 매우 쉽지만(비트 배열의 특정 인덱스 값이 참인지 거짓인지만 구분하면 되니까요), 특정 범위의 소수 개수를 구한다던지, 소수의 목록을 구하는 일은 비교적 효율이 떨어지게 됩니다. 왜냐하면, 반복문을 이용하여 원하는 범위 내의 비트 배열 내의 모든 비트들을 순회해야 하기 때문입니다.

예를 들어, 원하는 범위의 비트 배열의 길이가 32라면 32번 반복을 통해 각 비트의 값을 살펴봐야 합니다. 오늘은 이 문제점을, 비트연산을 적극적으로 활용하여 최적화 하는 방법에 대해 알아보도록 하겠습니다(전체 소스코드에 대한 설명은 생략하고 원리 위주로 설명하도록 하겠습니다. 전체 소스코드는 한번 다운받아서 컴파일 & 실행 해보세요).

먼저 다음의 비트 연산을 잘 봐 주세요.

n & (n - 1);

이 문장이 이 글의 핵심 코드가 되겠습니다. 이 비트 연산을 활용하면 비트 배열에서 1의 값을 갖는 비트만 순회할 수 있습니다. 어떤 원리로 그렇게 되는지 지금부터 살펴봅시다.

먼저 우리에게 익숙한 10진수를 가지고 생각해 보겠습니다. 다음과 같이 0과 1로만 이루어진 10진수가 있다고 합시다.

100101000000

여기에서 1을 빼면 다음처럼 될 것입니다.

100100999999

저 둘을 잘 봅시다. 특히 빨간색으로 강조된 부분을 잘 보세요.

100101000000
100100999999

몇 가지 다른, 0과 1만으로 이루어진 10진수들도 1을 뺀 후 원래의 수와 비교를 해봅시다.

1000000
0999999

110000110000
110000109999

이들을 잘 관찰해 보면, 0과 1만으로 이루어진 10진수에서 1을 빼면, 1 값을 갖는 가장 낮은 자릿수가 0으로 바뀌고, 그보다 낮은 모든 자릿수들은 0에서 9로(9는 10 - 1에서 왔습니다) 바뀐것을 알 수 있습니다.

사실 이것은 모든 기수법에 해당되는 이야기 인데, 일반화를 시켜보면, "0과 1로만 이루어진 n진수의 수 k가 있을 때, (k - 1)은, k 에서 1 값을 갖는 가장 낮은 자릿수를 0으로 만들고, 그보다 낮은 모든 자릿수들은 0에서 (n - 1)로 바꾼것과 같다." 가 됩니다.

자 이제 이 규칙을 2진수에 적용해 봅시다. 이때, 모든 2진수는 0과 1로만 이루어져 있고, (n - 1)에서 2진수의 경우 n이 2이므로, (n - 1) == 1이 됩니다. 따라서 다음과 같이 말할 수 있습니다.

"어떤 2진수 k가 있을 때, (k - 1)은, k에서 1 값을 갖는 가장 낮은 자릿수를 0으로 만들고, 그보다 낮은 모든 자릿수들은 0에서 1로 바꾼것과 같다."

자 이제, 아까 봤었던 0과 1로만 이루어진 10진수를 이제 2진수라고 생각하고, 원래의 수와 1을 뺀 수를 비교해 보도록 합시다.

100101000000
100100111111

1000000
0111111

110000110000
110000101111

이 이진수들을 가지고 비트 and 연산을 해 보겠습니다(n & (n - 1)).

100101000000
100100111111 &
----------------------------
100100000000

1000000
0111111 &
----------------------------
0000000

110000110000
110000101111 &
----------------------------
110000100000

1 값을 갖는 가장 낮은 자릿수(빨간색으로 표시된 1)가 0으로(파란색으로 표시된 0) 바뀐것을 볼 수 있습니다. 이 연산을 반복해 주면, 1 값을 갖는 자리수의 개수 만큼만 반복하여 값이 1인 자리수(비트)를 골라낼 수 있습니다.

이제 (n & (n - 1))의 연산 결과와 n에 비트 xor 연산을 적용하면, n에서 1의 값을 갖는 제일 낮은 자릿수 하나만을 골라낼 수 있게 됩니다.

100101000000
100100000000 ^
----------------------------
000001000000

1000000
0000000 ^
----------------------------
1000000

110000110000
110000100000 ^
----------------------------
000000010000

이것으로만 끝나면 좋겠지만, 문제가 한가지 더 있습니다. 우리는 특정 자릿수가 1인지는 식별할 수 있었지만, 그 자릿수가 비트 배열에서 몇 번 인덱스를 갖는지를 알아내지 못했습니다. 에라토스테네스의 체를 비트 단위로 쪼개서 구현하면, 어떤 정수 n이 소수인지를 담는 bool값이 비트 배열의 인덱스 n위치에 담기게 되므로, 비트 배열에서 값이 1인 원소의 인덱스를 구해내야 할 필요가 있습니다. 그리고 여기에는 값비싼 연산인 log₂연산, 혹은 비트 순회가 필요합니다. 비트 순회가 빠를 것 같지만 이렇게 하면, 모든 비트를 살펴보아야 했던 원래의 문제로 되돌아 가는 꼴이 됩니다.

하지만 여기에도 비트 연산을 잘 활용하여 최적화된 log₂연산을 구현하는 것이 가능합니다. 우리는 위에서 살펴본 ((n & (n - 1)) ^ n) 연산을 통해 원하는 자릿수 딱 하나만 1이고 나머지 자릿수는 모두 0으로 이루어진 값을 쉽게 구해낼 수 있었습니다. 여기서 1인 자릿수가 딱 하나밖에 없다는 점을 적극 활용하여 log₂를 구현해 보도록 합시다.

간단하게 8비트 정수값을 가지고 생각해 봅시다(지금부터 나오는 n은 모두 1인 비트가 하나뿐인 정수들입니다).

0b11110000(C++언어에서 0b 접두사는 2진수를 의미합니다)
만일 어떤 8비트 수 n과 위의 이진수의 비트 AND 연산 결과가 0이 아니라면, n은 2^4(0b00010000) 이상이라는 의미로 해석할 수 있습니다. 반대로 결과가 0이 나왔다면 n은 2^4 미만이라는 이야기가 됩니다. 이 때 0이 아닌 결과가 나왔다면, 결과값을 담을 변수(초기값0) r에 4를 더합니다.

자 이제 n이 2^4 이상이라는 결과가 나왔을 경우 다음 과정을 생각해 봅시다.

0b11000000
위의 이진수와 n의 비트 AND 연산 결과가 0이 아닌 값이 나왔다면, n은 2^6(0b01000000) 이상이라는 뜻이 됩니다. 그럼 r에 6을 더해줘야 할까요? 아닙니다. 2^4 이상이라는 사실이 판명된 시점에서 4를 이미 더했기 때문에 r에는 2만 더해주면 됩니다.

이제 n이 2^4 미만이라는 결과가 나왔을 경우 다음 과정도 생각해 봅시다.

0x00001100
위의 이진수와 n의 비트 AND 연산 결과가 0이 아니라면, n은 2^2(0b00000100) 이상이라는 뜻이 됩니다. 이번에는 r에 그냥 2를 더해주면 되겠군요.

2^4 이상인 경우와 2^4 미만인 경우 모두 이후 과정에서 0이 아닌 결과가 나오면 2를 더해주고 있습니다. 그래서 그냥 두 과정을 하나로 합쳐버립시다. 이것이 가능한 이유는, 2^4 이상인 경우와 2^4 미만인 경우가 겹치지 않고 상호 독립적인 데다가, 0이 아닌 결과가 나왔을 경우의 동작이 같기 때문입니다. 둘을 합쳐버린 결과를 봅시다.

0b11001100
위의 이진수와 n의 비트 AND 연산 결과가 0이 아닌 값이 나왔다면, r에 2를 더해줍니다.

이제 이것을 재귀적으로 반복해 주면 됩니다. 전체 과정은 다음과 같습니다.

1. r을 0으로 초기화 합니다.
2. 0b11110000과 n의 비트 AND 연산 결과가 0이 아니라면, r에 4를 더해줍니다.
3. 0b11001100과 n의 비트 AND 연산 결과가 0이 아니라면, r에 2를 더해줍니다.
4. 0b10101010과 n의 비트 AND 연산 결과가 0이 아니라면, r에 1을 더해줍니다.
5. 이제 r에는 log₂(n)의 값이 들어있습니다.

이제 얼마나 개선되었는지 테스트를 해봐야겠죠? 다음 테스트 결과들은 첨부파일에 업로드 되어 있는 소스코드를 실행한 결과물입니다. 해당 소스코드에는, 열심히해보자님의 깃허브에서 가져온 코드들 중, fastPrime.cpp 파일에서 그대로 가져온 코드와, 제가 작성한 성능개선 함수들이 모두 담겨 있습니다. 모든 테스트 결과는 위가 개선 전, 아래가 개선 후 입니다.

테스트 1.
1000000000121 -> 10000000000000481 -> 18446744073709551557 -> 18446744073709551533 -> 18446744073709551521 순서로 소수 판별하기




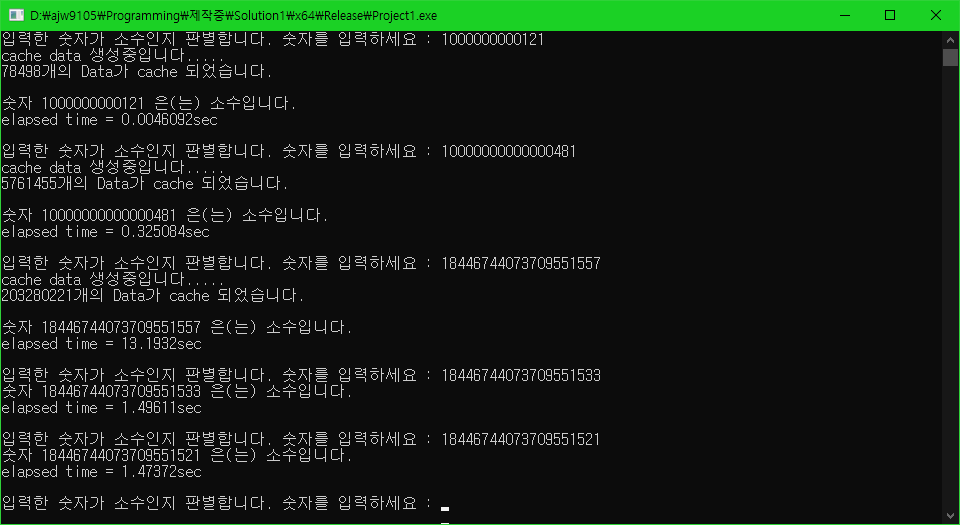
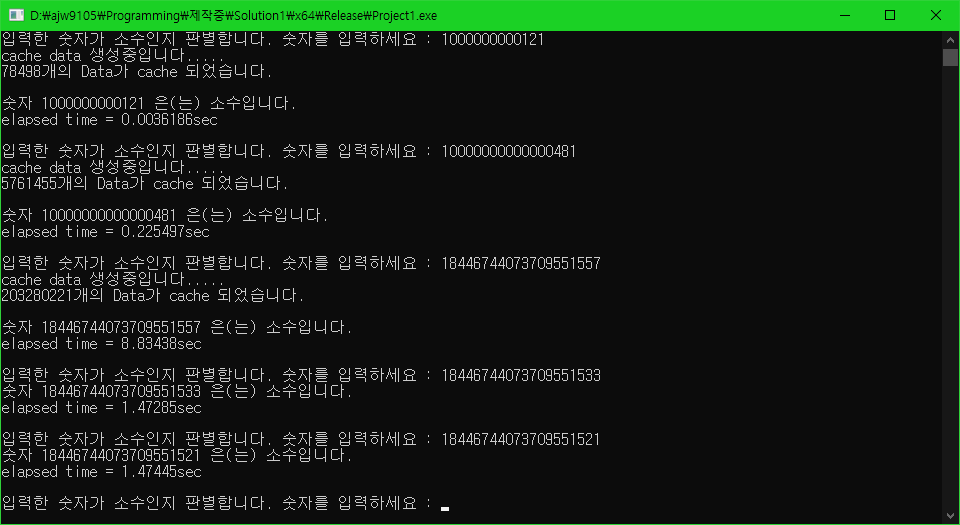
테스트 2.
1000000000121 -> 1000000000121 -> 10000000000000481 -> 10000000000000481 -> 18446744073709551557 -> 18446744073709551557 순서로 소수 판별하기




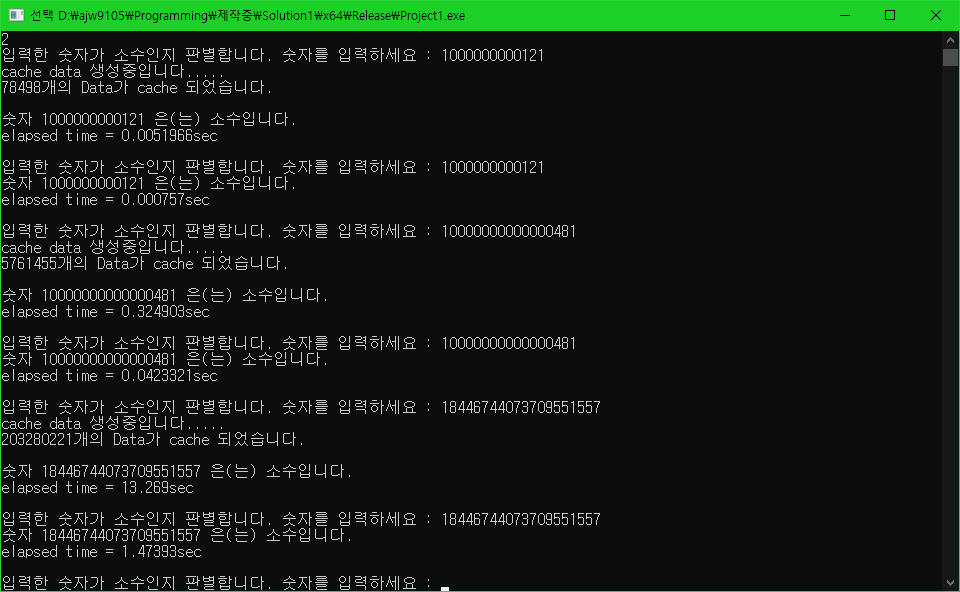
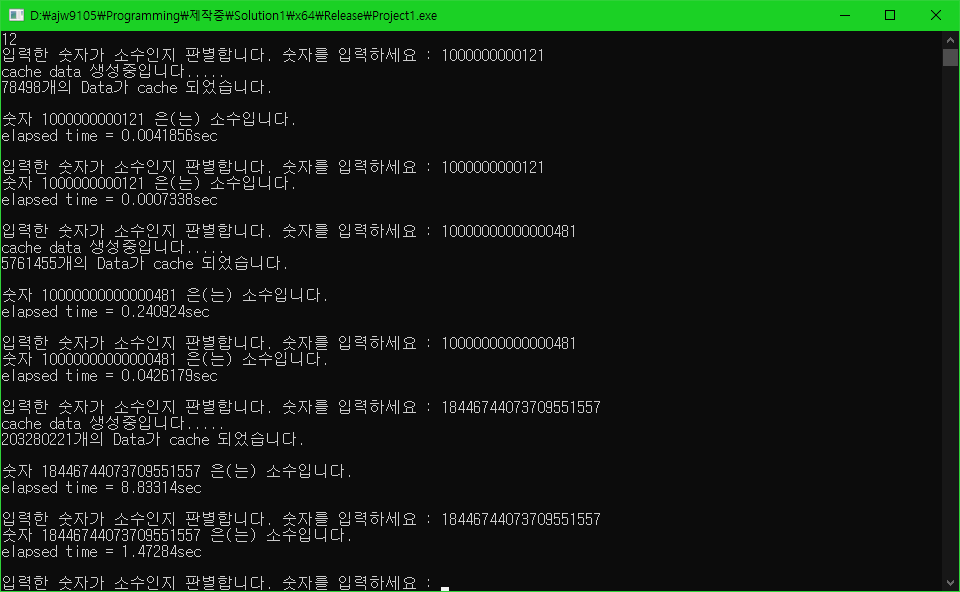
테스트 3.
10099999999997 -> 2305843009213693951 순서로 소수 판별하기




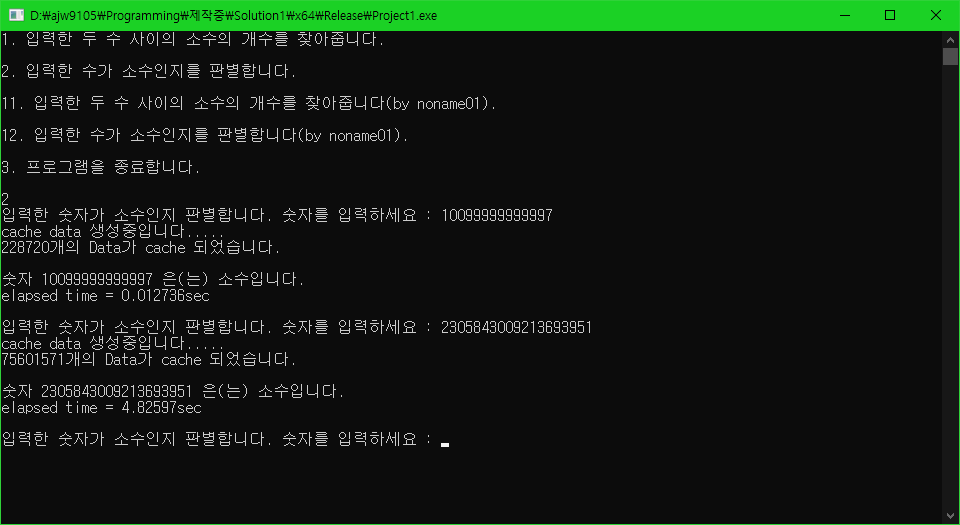
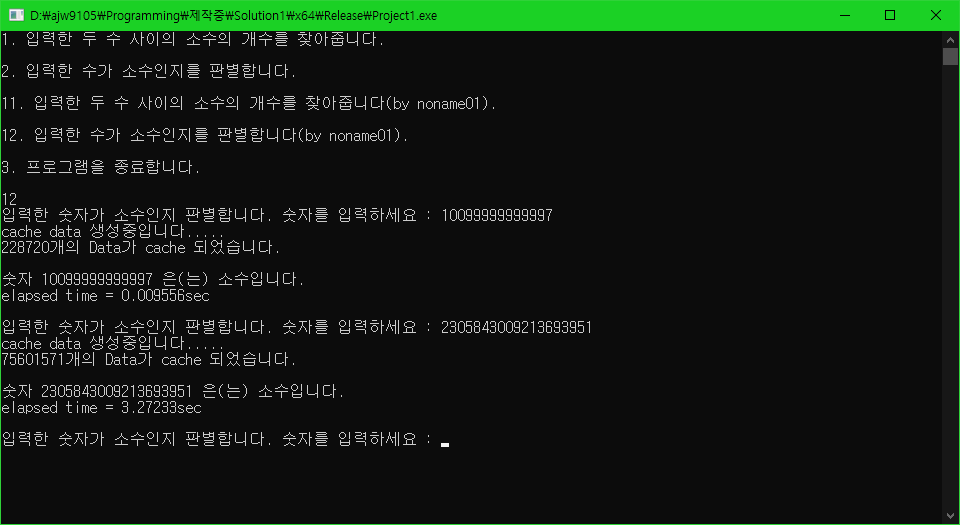
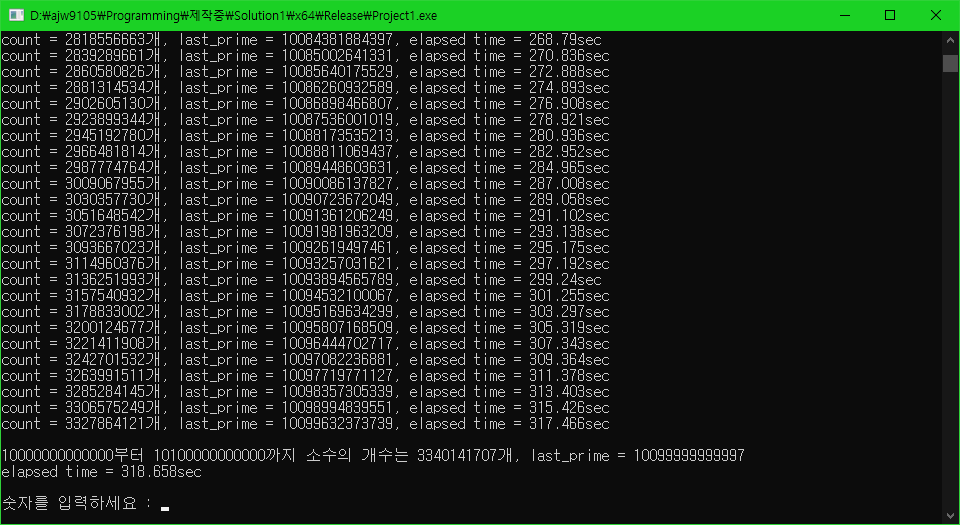
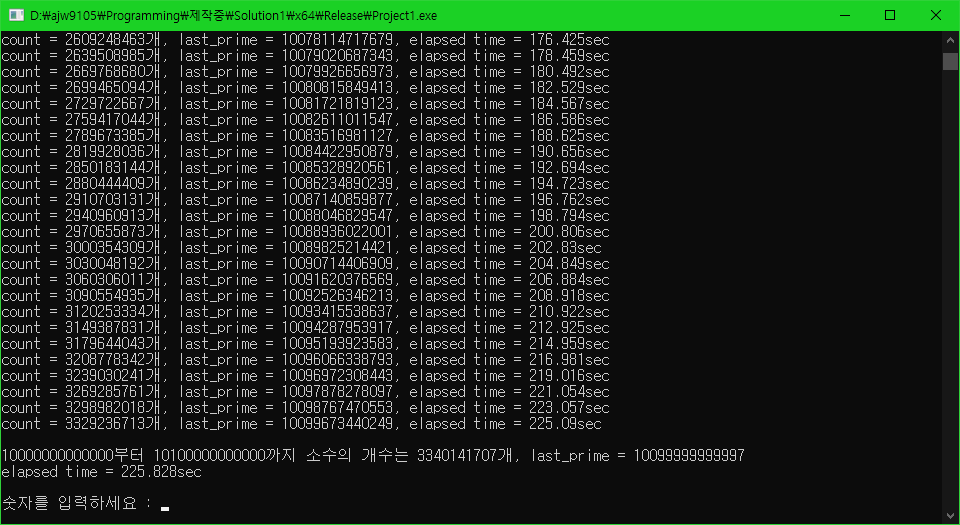
테스트 4.
10000000000000 ~ 10100000000000 범위의 소수 개수 구하기




테스트 5.
100000000000000000 ~ 100000100000000000 범위의 소수 개수 구하기




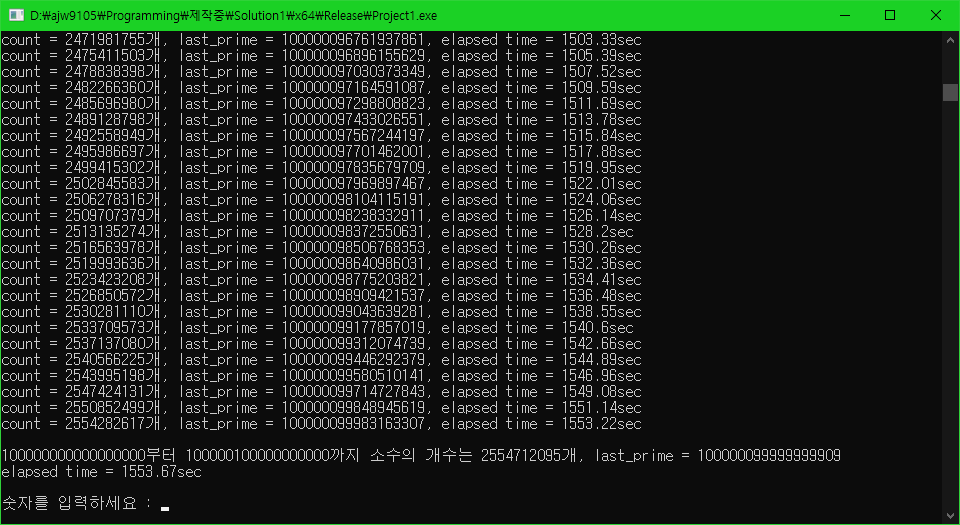
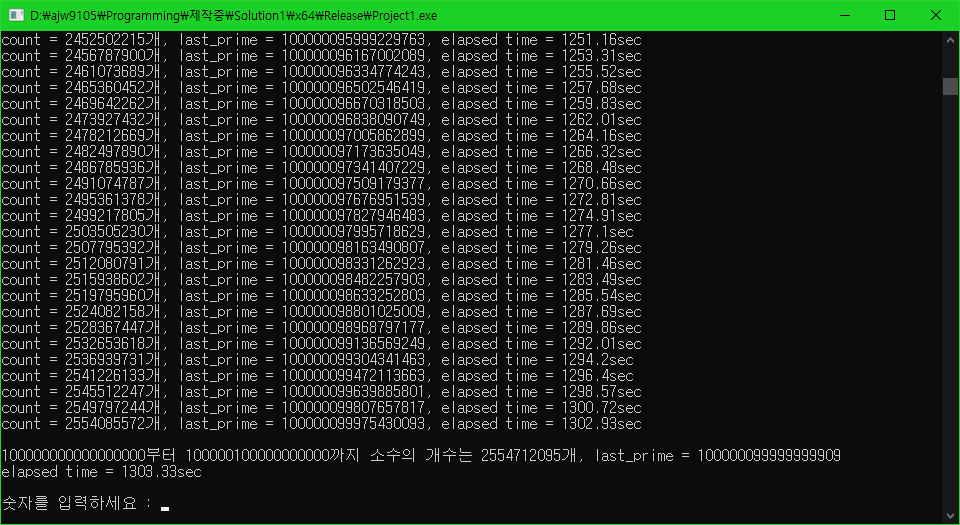
캐시를 구하거나 범위 내의 소수 개수를 구하는 데는 성능 향상이 있지만, 이미 캐시된 데이터들을 활용하여 소수를 판별하는데는 큰 차이가 없음을 볼 수 있습니다.